fidzu : software

Algorithms exploit dopamine hits for engagement. AI slop is everywhere. Mainstream media is agenda-driven. You are busy as it is. What is the healthy information diet you can stick to? In the last two years, I found excellent options that work great for me. Discover them in this post.

Surround yourself with great people. Use quality information. Garbage in, garbage out. If 90% of what you read or watch is optimized for widespread appeal, lacking nuance, optimized for tribal appeal and memetic survival, etc, you rot your brain. You undermine your world model, your decision-making ability, and your effectiveness.

Recommendations

First place goes to Scott Alexander and his Astral Codex Ten blog (formerly Slate Star Codex). Scott's essays are great for learning new concepts and levelling up your mental operating system, especially if you are new to the topics he covers. I started "reading" most posts once I discovered that there is a narrated audio version available on all the usual podcast platforms, including Spotify. My favourite post is from 2014, the famous Mediations on Moloch (audio).

Another favourite of mine is LessWrong. In particular, the Curated and Popular audio version. LessWrong is a community blog with high-quality posts on decision-making, epistemology, and AI safety/alignment. The Curated and Popular feed gives you a mix of evergreen concepts and reactions to recent events. Some random posts I linked and remember: Survival without dignity (hilarious), The Value Proposition of Romantic Relationships, Humans are not automatically strategic, and The Memetics of AI Successionism. Also worth a mention are The Sequences, especially the first few posts or the highlights, and The Best of LessWrong.

For recent events specifically, Don't Worry About the Vase is an excellent blog. Zvi, the prolific author of said blog, posts weekly AI roundups and provides early reactions to notable events within a day or so. It recently occurred to me that Don't Worry About the Vase is the closest thing I consume to a classical news channel. I like how Zvi incorporates quotes and back-and-forths from various sources, often with his perspective or response included. While this blog focuses on AI, other topics range from education to dating, and from movies to policy. There is an excellent audio version.

List

My favourite and common information sources:

• Astral Codex Ten blog (audio)
• LessWrong forum (audio)
• Don't Worry About the Vase blog (audio)
• Dwarkesh Podcast. My top podcast pick. Excellent guests.

Less frequent podcasts:

• No Priors - The hosts are VCs that interview builders and CEOs. Focus on AI and tech startups
• Moonshots - This is my feel-good entertainment podcast. Less signal. Extreme techno-optimism and dismantling the moon
• Mindscape - Sean Carroll (theoretical physicist) talks with guests about the nature of reality
• Naval - Timeless principles about high-agency and long-term focus. Minor focus on wealth. Infrequent content
• 80000 hours - Deep dives into topics surrounding saving the world and Effective Altruism. Warning: can be overly lengthy
• Y Combinator Startup Podcast - It's in the name, though recently it also includes terrible AI safety takes by Garry Tan
• Win-Win - Exploration of game theory, cooperation, incentives. The host has read Meditations on Moloch too many times

What's With All The Audio Links?

As I spend enough time looking at screens and reading, being able to consume blogs, articles, and podcasts via audio is great. One of my favourite activities is walking in the park with a good episode on, and doing laundry has never been this much fun.

I started out using Spotify, but switched to AntennaPod a few months ago. You can download this open-source podcast player for free. It's shown in the screenshot, and I can recommend it.

Twitter, No Wait X

Here are 10 X accounts you can follow for high-signal:

• Scott Alexander (@slatestarcodex) - Mentioned above, Astral Codex Ten author
• Eliezer Yudkowsky (@ESYudkowsky) - The final boss of rationalism, author of The Sequences
• Vitalik Buterin (@VitalikButerin) - Ethereum founder, 500IQ, decentralization freedmons n stuffs
• Zvi Mowshowitz (@TheZvi) - Mentioned above, don't Worry About the Vase author
• Aella (@Aella_Girl) - Prostitute statistician
• Rob Wiblin (@robertwiblin) - 80000 Hours podcast host
• Liv Boeree (@Liv_Boeree) - Win-Win podcast host
• Robin Hanson (@robinhanson) - Came up with Great Filter, Prediction Markets, Grabby Aliens, and more
• Andrej Karpathy (@karpathy) - AI researcher
• Ilya Sutskever (@ilyasut) - AI researcher

Turns out a lot of the people I consider high-signal are only on X. Seems like they haven't been knocked around much by the culture wars. Hence, this is a list of X accounts. In an effort to reduce the negative effects of The Algorithm and wasting time on noise, I created a list of X accounts, which I named Signal. This way can easily restrict my feed to only posts from these accounts. I keep this Signal list concise, at 10-15 accounts, many of which are listed above.

Including Robin Hanson here reminded me of Manifold Markets, which I am giving this honourable mention as a decent news source.

Your Top Picks?

What are your favourite sources of high-quality content? Let me know in the comments!

This post is a spiritual successor to my old Year In Books posts (2017, 2016, 2015). I've been thinking about posting another one of these for over 12 months. Since I "read" more via the sources mentioned in this post than classical books, and this seems like the more interesting topic for readers, you get this post instead.

The post High Density Information Sources in 2026 appeared first on Blog of Jeroen De Dauw.

19 Jan 2026 10:59am GMT

Pretty sure no-one is waiting for this, but after having spent a couple of years on the Fediverse (Mastodon in my case) I decided to add ActivityPub support to my WordPress installation via the ActivityPub plugin. I have the WP Rest Cache plugin active, so I'm expecting things to gently hum along, without (most likely) or with these posts gaining traction. Kudo's to Stian and Servebolt for…

Source

19 Jan 2026 10:59am GMT

Drupal turns 25 today. A quarter of a century.

What started as a hobby became a community, and then, somehow, a pillar of the web's infrastructure.

Looking back, the most important things I learned weren't really about software. They were about people, scale, and what it takes to build something that lasts.

Twenty-five years, twenty-five lessons.

At DrupalCon Paris 2009, we cut a ribbon. Druplicon was holding rather large scissors. The photo was taken at exactly the wrong moment, but it's still one of my favorite Drupal photos.

1. You can do well and do good

I used to think I had to choose: build a sustainable business or build something generous. Drupal taught me that is a false choice. Growth and generosity can reinforce each other. The real challenge is making sure one does not crowd out the other.

2. You can architect for community

Community doesn't just happen. You have to design for it. Drupal's modular system created clear places to contribute, our open logo invited people to make their own variants, and our light governance made it easy for people to step into responsibility. You cannot force a community to exist, but you can create the conditions for one to grow.

3. A few decisions define everything

Most choices don't matter much in hindsight, but a few end up shaping a project's entire trajectory. For Drupal, that included licensing under the GPL, the hook system, the node system, starting the Drupal Association, and even the credit system. You never know which decisions those are when you're making them.

4. Coordination is the product

In the early days, coordination was easy: you knew most people by name and you could fix things in a single late night IRC conversation. Then Drupal grew, slowly at first and then all at once. I remember release cycles where the hardest part was not the code but aligning hundreds of people across time zones, cultures and priorities, with far too much energy spent "bike shedding". That is when I learned that at scale, code is not the product. It is what we ship, but coordination is what makes it possible.

5. Everyone's carrying something

I've worked with people navigating challenges I couldn't see at first. Mental health struggles, caregiving burdens, personal crises. It taught me that someone's behavior in a moment rarely tells the whole story. A healthy community makes room for people. Patience and grace are how you keep good people around.

6. Nobody fully understands Drupal anymore, including me

After 25 years and tens of thousands of contributors, Drupal has grown beyond any single person's understanding. I also google Drupal's documentation. I'm strangely proud of that, because it's how I know it has become something bigger than any one of us.

7. Volunteerism alone doesn't scale

In the early years, everything in Drupal was built by volunteers, and for a long time that felt like enough. At some point, it wasn't. The project was growing faster than the time people could give, and some important work needed more hands. Paid contributors brought stability and depth, while volunteers continued to innovate. The best projects make room for both.

8. Your words carry more weight than you realize

As recently as a few weeks ago, I sent a Slack message I thought was harmless and watched it create confusion and frustration. I have been making that same mistake, in different forms, for years. As a project grows, so does the gravity of what you say. A passing comment can redirect weeks of work or demoralize someone who is trying their best. I had to learn to speak more carefully, not because I am important, but because my role is. I am still learning to do this better.

9. Maintenance is leadership with no applause

The bottleneck in Open Source is rarely new ideas or new code. It's people willing to maintain what already exists: reviewing, deciding, onboarding new people, and holding context for years. I have seen projects stall because nobody wanted to do that work, and others survive because a few people quietly stepped up. Maintainers do the work that keeps everything together. If you want a project to last, you have to take care of your maintainers.

10. Culture is forged under stress

The Drupal community was not just built on good vibes. It was built in the weeks before releases and DrupalCons, in late night debugging sessions, and in messy moments of disagreement and drama. I have seen stress bring out the best in us and, sometimes, the worst. Both mattered because they forced us to learn how to disagree, decide, and recover. Those hard moments forged trust you cannot manufacture in calm times, and they are a big reason the community is still here.

11. Leadership has to outgrow its founder

For Drupal to last, leadership had to move beyond me, and for that to happen I had to let go. That meant stepping back from decisions I cared deeply about and trusting others to take the project in directions I might not have chosen. There were moments when I felt sidelined in the project I started, which was nobody's fault, but not easy. Letting go was not always easy, but it is one of the reasons Drupal is still here.

12. Open source is not a meritocracy

I used to say that the only real limitation to contributing was your willingness to learn. I was wrong. Free time is a privilege, not an equal right. Some people have jobs, families, or responsibilities that leave no room for unpaid work. You can only design for equity when you stop pretending that Open Source is a meritocracy.

13. Changing your mind in public builds trust

Over the years, I've had to reverse positions I once argued for. Doing that in public taught me that admitting you were wrong builds more trust than claiming you were right. People remember how you handle being wrong longer than they remember what you were wrong about.

14. Persistence beats being right early

In 2001, Open Source was a curiosity that enterprises avoided. Today, it runs the world. I believed in it long before I could prove it. I kept working on Drupal anyway. It took many years for the world to catch up. That taught me that sticking with something you believe in matters more than being right quickly.

15. The hardest innovation is not breaking things

For years, I insisted that breaking backward compatibility was a core value. Upgrades were painful, but I thought that was the price of progress. The real breakthrough came when we built enough test coverage to keep moving forward without breaking what people had built. Today, Drupal has more than twice as much test code as production code. That discipline was harder than any rewrite, and it earned more trust than any new feature.

16. Most people are here for the right reasons

Every large community has bad actors and trolls, and they can consume all your attention if you let them. If you focus too much on the worst behavior, you start to miss the quiet, steady work of the many people who are here to build something good. Your energy is better spent supporting those people.

17. Talk is silver, contribution is gold

Words matter. They set direction and invite people in. But the people who shaped Drupal most were the ones who kept showing up to do the work. Culture is shaped by what actually gets done, and by who shows up to do it.

18. Vision doesn't have to come from the top

For a long time, I thought being project lead meant having the vision. Over time, I learned that it meant creating the conditions for good ideas to come from anywhere. The best decisions often came from people I'd never met, solving problems I didn't know we had.

19. The spark is individual but the fire is not

A single person can change a project's direction, but no contribution survives on its own. Every new feature comes with a maintenance cost and eventually depends on people the original author will never meet. Successful projects have to hold both truths at once: the spark is individual, but the fire is not.

20. At scale, even your bugs become features

Once enough people depend on your software, every observable behavior becomes a commitment, whether you intended it or not. Sooner or later, someone will build a workflow around an edge case or quirk. That is why maintaining compatibility is not a lesser form of work. It is core to the product.

21. A good project is measured by what people build next

For a long time, it felt like a loss when top contributors moved on from Drupal. Over time, I started to notice what they built next and realized they were carrying what they learned here into everything they did. Many went on to lead teams, start companies, or lead other Open Source projects. I have come to see that as one of Drupal's most meaningful outcomes.

22. Longevity comes from not chasing trends

Drupal is still here because we resisted the urge to chase every new trend and kept building on things that last, like structured content, security, extensibility, and openness. Those things mattered twenty years ago, they still matter today, and they will still matter twenty years from now.

23. If it matters, keep saying it

A community isn't a room. People join at different times, pay attention to different things, and hear through different filters. An idea has to land again and again before it takes hold. If it matters, keep saying it. The ideas that stick are the ones the community picks up and carries forward.

24. It takes a community to see the whole road

Sometimes the path forward seems clear. An individual can see a direction, but a community sees the terrain: the cracks, the forks, and the doubts. Being right alone brings clarity. Bringing others along brings confidence.

25. Start before you feel ready

When I released Drupal 1.0.0, I knew almost nothing. For much of the journey, I felt out of my depth. I was often nervous, sometimes intimidated. I didn't know how to scale software, how to build a community, or how to lead. I kept shipping anyway. You don't become ready by waiting. You become ready by doing.

A group photo taken at DrupalCon Seattle in 2019.

For those who have been here for years, these lessons will feel familiar. We learned them together, sometimes slowly, sometimes through debate, and often the hard way.

If Drupal has been part of your daily life for a long time, you are not just a user or a contributor. You are part of its history. And for all of you, I am grateful.

I am still here, still learning, and still excited about what we can build together next. Thank you for building it with me.

19 Jan 2026 10:59am GMT

I'm going to FOSDEM 2026!

I'm presenting in the Containers dev room. My talk is Java Memory Management in Containers and it's scheduled as the first talk on the first day. I'm the warm-up act!

The Java devroom has been a stalwart at FOSDEM since 2004 (sometimes in other forms), but sadly there's no Java devroom this year. There's a story about that, but it's not mine to tell.

Please recommend to me any interesting talks! Here's a few that caught my eye:

Debian/related:

• Package managers à la carte: A Formal Model of Dependency Resolution
• 32 years of Debian: how a do-ocracy keeps evolving
• Free as in Burned Out: Who Really Pays for Open Source?

Containers:

• Who's reproducing the reproducible images?

Research:

• Data science from the command line: a look back at 2 years of using xan
• Research software engineering: a movement and its instantiation at the University of Illinois Urbana-Champaign

Other:

• Window Managers after Xorg (Mir)
• Charming Gray Buttons of the XX century: how widget toolkits evolved with computer architectures
• PAW, a programmable DAW

19 Jan 2026 9:52am GMT

The Aim

I have just got a Furilabs FLX1s [1] which is a phone running a modified version of Debian. I want to have a phone that runs all apps that I control and can observe and debug. Android is very good for what it does and there are security focused forks of Android which have a lot of potential, but for my use a Debian phone is what I want.

The FLX1s is not going to be my ideal phone, I am evaluating it for use as a daily-driver until a phone that meets my ideal criteria is built. In this post I aim to provide information to potential users about what it can do, how it does it, and how to get the basic functions working. I also evaluate how well it meets my usage criteria.

I am not anywhere near an average user. I don't think an average user would ever even see one unless a more technical relative showed one to them. So while this phone could be used by an average user I am not evaluating it on that basis. But of course the features of the GUI that make a phone usable for an average user will allow a developer to rapidly get past the beginning stages and into more complex stuff.

Features

The Furilabs FLX1s [1] is a phone that is designed to run FuriOS which is a slightly modified version of Debian. The purpose of this is to run Debian instead of Android on a phone. It has switches to disable camera, phone communication, and microphone (similar to the Librem 5) but the one to disable phone communication doesn't turn off Wifi, the only other phone I know of with such switches is the Purism Librem 5.

It has a 720*1600 display which is only slightly better than the 720*1440 display in the Librem 5 and PinePhone Pro. This doesn't compare well to the OnePlus 6 from early 2018 with 2280*1080 or the Note9 from late 2018 with 2960*1440 - which are both phones that I've run Debian on. The current price is $US499 which isn't that good when compared to the latest Google Pixel series, a Pixel 10 costs $US649 and has a 2424*1080 display and it also has 12G of RAM while the FLX1s only has 8G. Another annoying thing is how rounded the corners are, it seems that round corners that cut off the content are a standard practice nowadays, in my collection of phones the latest one I found with hard right angles on the display was a Huawei Mate 10 Pro which was released in 2017. The corners are rounder than the Note 9, this annoys me because the screen is not high resolution by today's standards so losing the corners matters.

The default installation is Phosh (the GNOME shell for phones) and it is very well configured. Based on my experience with older phone users I think I could give a phone with this configuration to a relative in the 70+ age range who has minimal computer knowledge and they would be happy with it. Additionally I could set it up to allow ssh login and instead of going through the phone support thing of trying to describe every GUI setting to click on based on a web page describing menus for the version of Android they are running I could just ssh in and run diff on the .config directory to find out what they changed. Furilabs have done a very good job of setting up the default configuration, while Debian developers deserve a lot of credit for packaging the apps the Furilabs people have chosen a good set of default apps to install to get it going and appear to have made some noteworthy changes to some of them.

Droidian

The OS is based on Android drivers (using the same techniques as Droidian [2]) and the storage device has the huge number of partitions you expect from Android as well as a 110G Ext4 filesystem for the main OS.

The first issue with the Droidian approach of using an Android kernel and containers for user space code to deal with drivers is that it doesn't work that well. There are 3 D state processes (uninterrupteable sleep - which usually means a kernel bug if the process remains in that state) after booting and doing nothing special. My tests running Droidian on the Note 9 also had D state processes, in this case they are D state kernel threads (I can't remember if the Note 9 had regular processes or kernel threads stuck in D state). It is possible for a system to have full functionality in spite of some kernel threads in D state but generally it's a symptom of things not working as well as you would hope.

The design of Droidian is inherently fragile. You use a kernel and user space code from Android and then use Debian for the rest. You can't do everything the Android way (with the full OS updates etc) and you also can't do everything the Debian way. The TOW Boot functionality in the PinePhone Pro is really handy for recovery [3], it allows the internal storage to be accessed as a USB mass storage device. The full Android setup with ADB has some OK options for recovery, but part Android and part Debian has less options. While it probably is technically possible to do the same things in regard to OS repair and reinstall the fact that it's different from most other devices means that fixes can't be done in the same way.

Applications

GUI

The system uses Phosh and Phoc, the GNOME system for handheld devices. It's a very different UI from Android, I prefer Android but it is usable with Phosh.

IM

Chatty works well for Jabber (XMPP) in my tests. It supports Matrix which I didn't test because I don't desire the same program doing Matrix and Jabber and because Matrix is a heavy protocol which establishes new security keys for each login so I don't want to keep logging in on new applications.

Chatty also does SMS but I couldn't test that without the SIM caddy.

I use Nheko for Matrix which has worked very well for me on desktops and laptops running Debian.

Email

I am currently using Geary for email. It works reasonably well but is lacking proper management of folders, so I can't just subscribe to the important email on my phone so that bandwidth isn't wasted on less important email (there is a GNOME gitlab issue about this - see the Debian Wiki page about Mobile apps [4]).

Music

Music playing isn't a noteworthy thing for a desktop or laptop, but a good music player is important for phone use. The Lollypop music player generally does everything you expect along with support for all the encoding formats including FLAC0 - a major limitation of most Android music players seems to be lack of support for some of the common encoding formats. Lollypop has it's controls for pause/play and going forward and backward one track on the lock screen.

Maps

The installed map program is gnome-maps which works reasonably well. It gets directions via the Graphhopper API [5]. One thing we really need is a FOSS replacement for Graphhopper in GNOME Maps.

Delivery and Unboxing

I received my FLX1s on the 13th of Jan [1]. I had paid for it on the 16th of Oct but hadn't received the email with the confirmation link so the order had been put on hold. But after I contacted support about that on the 5th of Jan they rapidly got it to me which was good. They also gave me a free case and screen protector to apologise, I don't usually use screen protectors but in this case it might be useful as the edges of the case don't even extend 0.5mm above the screen. So if it falls face down the case won't help much.

When I got it there was an open space at the bottom where the caddy for SIMs is supposed to be. So I couldn't immediately test VoLTE functionality. The contact form on their web site wasn't working when I tried to report that and the email for support was bouncing.

Bluetooth

As a test of Bluetooth I connected it to my Nissan LEAF which worked well for playing music and I connected it to several Bluetooth headphones. My Thinkpad running Debian/Trixie doesn't connect to the LEAF and to headphones which have worked on previous laptops running Debian and Ubuntu. A friend's laptop running Debian/Trixie also wouldn't connect to the LEAF so I suspect a bug in Trixie, I need to spend more time investigating this.

Wifi

Currently 5GHz wifi doesn't work, this is a software bug that the Furilabs people are working on. 2.4GHz wifi works fine. I haven't tested running a hotspot due to being unable to get 4G working as they haven't yet shipped me the SIM caddy.

Docking

This phone doesn't support DP Alt-mode or Thunderbolt docking so it can't drive an external monitor. This is disappointing, Samsung phones and tablets have supported such things since long before USB-C was invented. Samsung DeX is quite handy for Android devices and that type feature is much more useful on a device running Debian than on an Android device.

Camera

The camera works reasonably well on the FLX1s. Until recently for the Librem 5 the camera didn't work and the camera on my PinePhone Pro currently doesn't work. Here are samples of the regular camera and the selfie camera on the FLX1s and the Note 9. I think this shows that the camera is pretty decent. The selfie looks better and the front camera is worse for the relatively close photo of a laptop screen - taking photos of computer screens is an important part of my work but I can probably work around that.

I wasn't assessing this camera t find out if it's great, just to find out if I have the sorts of problems I had before and it just worked. The Samsung Galaxy Note series of phones has always had decent specs including good cameras. Even though the Note 9 is old comparing to it is a respectable performance. The lighting was poor for all photos.

FLX1s

Note 9

Power Use

In 93 minutes having the PinePhone Pro, Librem 5, and FLX1s online with open ssh sessions from my workstation the PinePhone Pro went from 100% battery to 26%, the Librem 5 went from 95% to 69%, and the FLX1s went from 100% to 99%. The battery discharge rate of them was reported as 3.0W, 2.6W, and 0.39W respectively. Based on having a 16.7Wh battery 93 minutes of use should have been close to 4% battery use, but in any case all measurements make it clear that the FLX1s will have a much longer battery life. Including the measurement of just putting my fingers on the phones and feeling the temperature (FLX1s felt cool and the others felt hot).

The PinePhone Pro and the Librem 5 have an optional "Caffeine mode" which I enabled for this test, without that enabled the phone goes into a sleep state and disconnects from Wifi. So those phones would use much less power with caffeine mode enabled, but they also couldn't get fast response to notifications etc. I found the option to enable a Caffeine mode switch on the FLX1s but the power use was reported as being the same both with and without it.

Charging

One problem I found with my phone is that in every case it takes 22 seconds to negotiate power. Even when using straight USB charging (no BC or PD) it doesn't draw any current for 22 seconds. When I connect it it will stay at 5V and varying between 0W and 0.1W (current rounded off to zero) for 22 seconds or so and then start charging. After the 22 second display the phone will make the tick sound indicating that it's charging and the power meter will measure that it's drawing some current.

I added the table from my previous post about phone charging speed [6] with an extra row for the FLX1s. For charging from my PC USB ports the results were the worst ever, the port that does BC did not work at all it was looping trying to negotiate after a 22 second negotiation delay the port would turn off. The non-BC port gave only 2.4W which matches the 2.5W given by the spec for a "High-power device" which is what that port is designed to give. In a discussion on the Purism forum about the Librem5 charging speed one of their engineers told me that the reason why their phone would draw 2A from that port was because the cable was identifying itself as a USB-C port not a "High-power device" port. But for some reason out of the 7 phones I tested the FLX1s and the One Plus 6 are the only ones to limit themselves to what the port is apparently supposed to do. Also the One Plus 6 charges slowly on every power supply so I don't know if it is obeying the spec or just sucking.

On a cheap AliExpress charger the FLX1s gets 5.9V and on a USB battery it gets 5.8V. Out of all 42 combinations of device and charger I tested these were the only ones to involve more than 5.1V but less than 9V. I welcome comments suggesting an explanation.

The case that I received has a hole for the USB-C connector that isn't wide enough for the plastic surrounds on most of my USB-C cables (including the Dell dock). Also to make a connection requires a fairly deep insertion (deeper than the One Plus 6 or the Note 9). So without adjustment I have to take the case off to charge it. It's no big deal to adjust the hole (I have done it with other cases) but it's an annoyance.

Conclusion

The Furilabs support people are friendly and enthusiastic but my customer experience wasn't ideal. It was good that they could quickly respond to my missing order status and the missing SIM caddy (which I still haven't received but believe is in the mail) but it would be better if such things just didn't happen.

The phone is quite user friendly and could be used by a novice.

I paid $US577 for the FLX1s which is $AU863 by today's exchange rates. For comparison I could get a refurbished Pixel 9 Pro Fold for $891 from Kogan (the major Australian mail-order company for technology) or a refurbished Pixel 9 Pro XL for $842. The Pixel 9 series has security support until 2031 which is probably longer than you can expect a phone to be used without being broken. So a phone with a much higher resolution screen that's only one generation behind the latest high end phones and is refurbished will cost less. For a brand new phone a Pixel 8 Pro which has security updates until 2030 costs $874 and a Pixel 9A which has security updates until 2032 costs $861.

Doing what the Furilabs people have done is not a small project. It's a significant amount of work and the prices of their products need to cover that. I'm not saying that the prices are bad, just that economies of scale and the large quantity of older stock makes the older Google products quite good value for money. The new Pixel phones of the latest models are unreasonably expensive. The Pixel 10 is selling new from Google for $AU1,149 which I consider a ridiculous price that I would not pay given the market for used phones etc. If I had a choice of $1,149 or a "feature phone" I'd pay $1,149. But the FLX1s for $863 is a much better option for me. If all I had to choose from was a new Pixel 10 or a FLX1s for my parents I'd get them the FLX1s.

For a FOSS developer a FLX1s could be a mobile test and development system which could be lent to a relative when their main phone breaks and the replacement is on order. It seems to be fit for use as a commodity phone. Note that I give this review on the assumption that SMS and VoLTE will just work, I haven't tested them yet.

The UI on the FLX1s is functional and easy enough for a new user while allowing an advanced user to do the things they desire. I prefer the Android style and the Plasma Mobile style is closer to Android than Phosh is, but changing it is something I can do later. Generally I think that the differences between UIs matter more when on a desktop environment that could be used for more complex tasks than on a phone which limits what can be done by the size of the screen.

I am comparing the FLX1s to Android phones on the basis of what technology is available. But most people who would consider buying this phone will compare it to the PinePhone Pro and the Librem 5 as they have similar uses. The FLX1s beats both those phones handily in terms of battery life and of having everything just work. But it has the most non free software of the three and the people who want the $2000 Librem 5 that's entirely made in the US won't want the FLX1s.

This isn't the destination for Debian based phones, but it's a good step on the way to it and I don't think I'll regret this purchase.

• [1] https://furilabs.com/shop/flx1s/
• [2] https://droidian.org/
• [3] https://wiki.debian.org/InstallingDebianOn/PINE64/PinePhonePro
• [4] https://wiki.debian.org/MobileApps
• [5] https://www.graphhopper.com/
• [6] https://etbe.coker.com.au/2026/01/05/phone-charging-speeds/

19 Jan 2026 6:43am GMT

Standard RAID solutions waste space when disks have different sizes. Linux software RAID with LVM uses the full capacity of each disk and lets you grow storage by replacing one or two disks at a time.

We start with four disks of equal size:

$ lsblk -Mo NAME,TYPE,SIZE
NAME TYPE  SIZE
vda  disk  101M
vdb  disk  101M
vdc  disk  101M
vdd  disk  101M

We create one partition on each of them:

$ sgdisk --zap-all --new=0:0:0 -t 0:fd00 /dev/vda
$ sgdisk --zap-all --new=0:0:0 -t 0:fd00 /dev/vdb
$ sgdisk --zap-all --new=0:0:0 -t 0:fd00 /dev/vdc
$ sgdisk --zap-all --new=0:0:0 -t 0:fd00 /dev/vdd
$ lsblk -Mo NAME,TYPE,SIZE
NAME   TYPE  SIZE
vda    disk  101M
└─vda1 part  100M
vdb    disk  101M
└─vdb1 part  100M
vdc    disk  101M
└─vdc1 part  100M
vdd    disk  101M
└─vdd1 part  100M

We set up a RAID 5 device by assembling the four partitions:¹

$ mdadm --create /dev/md0 --level=raid5 --bitmap=internal --raid-devices=4 \
>   /dev/vda1 /dev/vdb1 /dev/vdc1 /dev/vdd1
$ lsblk -Mo NAME,TYPE,SIZE
    NAME          TYPE    SIZE
    vda           disk    101M
┌┈▶ └─vda1        part    100M
┆   vdb           disk    101M
├┈▶ └─vdb1        part    100M
┆   vdc           disk    101M
├┈▶ └─vdc1        part    100M
┆   vdd           disk    101M
└┬▶ └─vdd1        part    100M
 └┈┈md0           raid5 292.5M
$ cat /proc/mdstat
md0 : active raid5 vdd1[4] vdc1[2] vdb1[1] vda1[0]
      299520 blocks super 1.2 level 5, 512k chunk, algorithm 2 [4/4] [UUUU]
      bitmap: 0/1 pages [0KB], 65536KB chunk

We use LVM to create logical volumes on top of the RAID 5 device.

$ pvcreate /dev/md0
  Physical volume "/dev/md0" successfully created.
$ vgcreate data /dev/md0
  Volume group "data" successfully created
$ lvcreate -L 100m -n bits data
  Logical volume "bits" created.
$ lvcreate -L 100m -n pieces data
  Logical volume "pieces" created.
$ mkfs.ext4 -q /dev/data/bits
$ mkfs.ext4 -q /dev/data/pieces
$ lsblk -Mo NAME,TYPE,SIZE
    NAME          TYPE    SIZE
    vda           disk    101M
┌┈▶ └─vda1        part    100M
┆   vdb           disk    101M
├┈▶ └─vdb1        part    100M
┆   vdc           disk    101M
├┈▶ └─vdc1        part    100M
┆   vdd           disk    101M
└┬▶ └─vdd1        part    100M
 └┈┈md0           raid5 292.5M
    ├─data-bits   lvm     100M
    └─data-pieces lvm     100M
$ vgs
  VG   #PV #LV #SN Attr   VSize   VFree
  data   1   2   0 wz--n- 288.00m 88.00m

This gives us the following setup:

RAID 5 setup with disks of equal capacity

We replace /dev/vda with a bigger disk. We add it back to the RAID 5 array after copying the partitions from /dev/vdb:

$ cat /proc/mdstat
md0 : active (auto-read-only) raid5 vdb1[1] vdd1[4] vdc1[2]
      299520 blocks super 1.2 level 5, 512k chunk, algorithm 2 [4/3] [_UUU]
      bitmap: 0/1 pages [0KB], 65536KB chunk
$ sgdisk --replicate=/dev/vda /dev/vdb
$ sgdisk --randomize-guids /dev/vda
$ mdadm --manage /dev/md0 --add /dev/vda1
$ cat /proc/mdstat
md0 : active raid5 vda1[5] vdb1[1] vdd1[4] vdc1[2]
      299520 blocks super 1.2 level 5, 512k chunk, algorithm 2 [4/4] [UUUU]
      bitmap: 0/1 pages [0KB], 65536KB chunk

We do not use the additional capacity: this setup would not survive the loss of /dev/vda because we have no spare capacity. We need a second disk replacement, like /dev/vdb:

$ cat /proc/mdstat
md0 : active (auto-read-only) raid5 vda1[5] vdd1[4] vdc1[2]
      299520 blocks super 1.2 level 5, 512k chunk, algorithm 2 [4/3] [U_UU]
      bitmap: 0/1 pages [0KB], 65536KB chunk
$ sgdisk --replicate=/dev/vdb /dev/vdc
$ sgdisk --randomize-guids /dev/vdb
$ mdadm --manage /dev/md0 --add /dev/vdb1
$ cat /proc/mdstat
md0 : active raid5 vdb1[6] vda1[5] vdd1[4] vdc1[2]
      299520 blocks super 1.2 level 5, 512k chunk, algorithm 2 [4/4] [UUUU]
      bitmap: 0/1 pages [0KB], 65536KB chunk

We create a new RAID 1 array by using the free space on /dev/vda and /dev/vdb:

$ sgdisk --new=0:0:0 -t 0:fd00 /dev/vda
$ sgdisk --new=0:0:0 -t 0:fd00 /dev/vdb
$ mdadm --create /dev/md1 --level=raid1 --bitmap=internal --raid-devices=2 \
>   /dev/vda2 /dev/vdb2
$ cat /proc/mdstat
md1 : active raid1 vdb2[1] vda2[0]
      101312 blocks super 1.2 [2/2] [UU]
      bitmap: 0/1 pages [0KB], 65536KB chunk

md0 : active raid5 vdb1[6] vda1[5] vdd1[4] vdc1[2]
      299520 blocks super 1.2 level 5, 512k chunk, algorithm 2 [4/4] [UUUU]
      bitmap: 0/1 pages [0KB], 65536KB chunk

We add /dev/md1 to the volume group:

$ pvcreate /dev/md1
  Physical volume "/dev/md1" successfully created.
$ vgextend data /dev/md1
  Volume group "data" successfully extended
$ vgs
  VG   #PV #LV #SN Attr   VSize   VFree
  data   2   2   0 wz--n- 384.00m 184.00m
$  lsblk -Mo NAME,TYPE,SIZE
       NAME          TYPE    SIZE
       vda           disk    201M
   ┌┈▶ ├─vda1        part    100M
┌┈▶┆   └─vda2        part    100M
┆  ┆   vdb           disk    201M
┆  ├┈▶ ├─vdb1        part    100M
└┬▶┆   └─vdb2        part    100M
 └┈┆┈┈┈md1           raid1  98.9M
   ┆   vdc           disk    101M
   ├┈▶ └─vdc1        part    100M
   ┆   vdd           disk    101M
   └┬▶ └─vdd1        part    100M
    └┈┈md0           raid5 292.5M
       ├─data-bits   lvm     100M
       └─data-pieces lvm     100M

This gives us the following setup:²

Setup mixing both RAID 1 and RAID 5

We extend our capacity further by replacing /dev/vdc:

$ cat /proc/mdstat
md1 : active (auto-read-only) raid1 vda2[0] vdb2[1]
      101312 blocks super 1.2 [2/2] [UU]
      bitmap: 0/1 pages [0KB], 65536KB chunk

md0 : active (auto-read-only) raid5 vda1[5] vdd1[4] vdb1[6]
      299520 blocks super 1.2 level 5, 512k chunk, algorithm 2 [4/3] [UU_U]
      bitmap: 0/1 pages [0KB], 65536KB chunk
$ sgdisk --replicate=/dev/vdc /dev/vdb
$ sgdisk --randomize-guids /dev/vdc
$ mdadm --manage /dev/md0 --add /dev/vdc1
$ cat /proc/mdstat
md1 : active (auto-read-only) raid1 vda2[0] vdb2[1]
      101312 blocks super 1.2 [2/2] [UU]
      bitmap: 0/1 pages [0KB], 65536KB chunk

md0 : active raid5 vdc1[7] vda1[5] vdd1[4] vdb1[6]
      299520 blocks super 1.2 level 5, 512k chunk, algorithm 2 [4/4] [UUUU]
      bitmap: 0/1 pages [0KB], 65536KB chunk

Then, we convert /dev/md1 from RAID 1 to RAID 5:

$ mdadm --grow /dev/md1 --level=5 --raid-devices=3 --add /dev/vdc2
mdadm: level of /dev/md1 changed to raid5
mdadm: added /dev/vdc2
$ cat /proc/mdstat
md1 : active raid5 vdc2[2] vda2[0] vdb2[1]
      202624 blocks super 1.2 level 5, 64k chunk, algorithm 2 [3/3] [UUU]
      bitmap: 0/1 pages [0KB], 65536KB chunk

md0 : active raid5 vdc1[7] vda1[5] vdd1[4] vdb1[6]
      299520 blocks super 1.2 level 5, 512k chunk, algorithm 2 [4/4] [UUUU]
      bitmap: 0/1 pages [0KB], 65536KB chunk
$ pvresize /dev/md1
$ vgs
  VG   #PV #LV #SN Attr   VSize   VFree
  data   2   2   0 wz--n- 482.00m 282.00m

This gives us the following layout:

RAID 5 setup with mixed-capacity disks using partitions and LVM

We further extend our capacity by replacing /dev/vdd:

$ cat /proc/mdstat
md0 : active (auto-read-only) raid5 vda1[5] vdc1[7] vdb1[6]
      299520 blocks super 1.2 level 5, 512k chunk, algorithm 2 [4/3] [UUU_]
      bitmap: 0/1 pages [0KB], 65536KB chunk

md1 : active (auto-read-only) raid5 vda2[0] vdc2[2] vdb2[1]
      202624 blocks super 1.2 level 5, 64k chunk, algorithm 2 [3/3] [UUU]
      bitmap: 0/1 pages [0KB], 65536KB chunk
$ sgdisk --replicate=/dev/vdd /dev/vdc
$ sgdisk --randomize-guids /dev/vdd
$ mdadm --manage /dev/md0 --add /dev/vdd1
$ cat /proc/mdstat
md0 : active raid5 vdd1[4] vda1[5] vdc1[7] vdb1[6]
      299520 blocks super 1.2 level 5, 512k chunk, algorithm 2 [4/4] [UUUU]
      bitmap: 0/1 pages [0KB], 65536KB chunk

md1 : active (auto-read-only) raid5 vda2[0] vdc2[2] vdb2[1]
      202624 blocks super 1.2 level 5, 64k chunk, algorithm 2 [3/3] [UUU]
      bitmap: 0/1 pages [0KB], 65536KB chunk

We grow the second RAID 5 array:

$ mdadm --grow /dev/md1 --raid-devices=4 --add /dev/vdd2
mdadm: added /dev/vdd2
$ cat /proc/mdstat
md0 : active raid5 vdd1[4] vda1[5] vdc1[7] vdb1[6]
      299520 blocks super 1.2 level 5, 512k chunk, algorithm 2 [4/4] [UUUU]
      bitmap: 0/1 pages [0KB], 65536KB chunk

md1 : active raid5 vdd2[3] vda2[0] vdc2[2] vdb2[1]
      303936 blocks super 1.2 level 5, 64k chunk, algorithm 2 [4/4] [UUUU]
      bitmap: 0/1 pages [0KB], 65536KB chunk
$ pvresize /dev/md1
$ vgs
  VG   #PV #LV #SN Attr   VSize   VFree
  data   2   2   0 wz--n- 580.00m 380.00m
$ lsblk -Mo NAME,TYPE,SIZE
       NAME          TYPE    SIZE
       vda           disk    201M
   ┌┈▶ ├─vda1        part    100M
┌┈▶┆   └─vda2        part    100M
┆  ┆   vdb           disk    201M
┆  ├┈▶ ├─vdb1        part    100M
├┈▶┆   └─vdb2        part    100M
┆  ┆   vdc           disk    201M
┆  ├┈▶ ├─vdc1        part    100M
├┈▶┆   └─vdc2        part    100M
┆  ┆   vdd           disk    301M
┆  └┬▶ ├─vdd1        part    100M
└┬▶ ┆  └─vdd2        part    100M
 ┆  └┈┈md0           raid5 292.5M
 ┆     ├─data-bits   lvm     100M
 ┆     └─data-pieces lvm     100M
 └┈┈┈┈┈md1           raid5 296.8M

You can continue by replacing each disk one by one using the same steps. ♾️

19 Jan 2026 5:49am GMT

FSet v2.2.0, which is the version included in the recent Quicklisp release, has a new Quicklisp-loadable system, FSet/Jzon. It extends the Jzon JSON parser/printer to construct FSet collections when reading, and to be able to print them.

On parsing, JSON arrays produce FSet seqs; JSON objects produce FSet replay maps by default, but the parser can also be configured to produce ordinary maps or FSet tuples. For printing, any of these can be handled, as well as the standard Jzon types. The tuple representation provides a way to control the printing of `nil`, depending on the type of the corresponding key.

For details, see the GitLab MR.

NOTE: unfortunately, the v2.1.0 release had some bugs in the new seq code, and I didn't notice them until after v2.2.0 was in Quicklisp. If you're using seqs, I strongly recommend you pick up v2.2.2 or newer from GitLab or GitHub.

16 Jan 2026 8:05am GMT

I wrote ILsee, an Interlisp source file viewer. It is the first of the ILtools collection of tools for viewing and accessing Interlisp data.

I developed ILsee in Common Lisp on Linux with SBCL and the McCLIM implementation of the CLIM GUI toolkit. SLY for Emacs completed my Lisp tooling and, as for infrastructure, ILtools is the first new project I host at Codeberg.

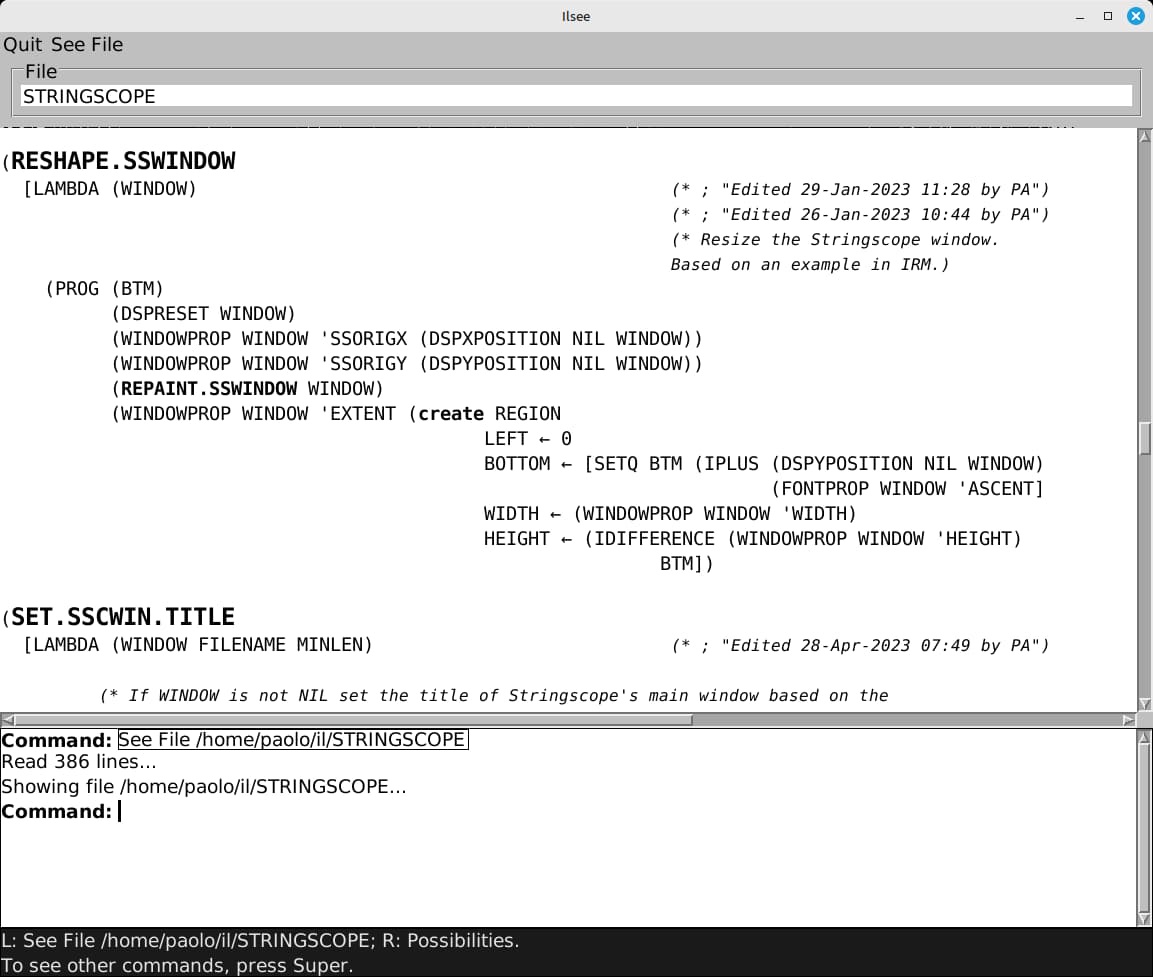
This is ILsee showing the code of an Interlisp file:

Motivation

The concepts and features of CLIM, such as stream-oriented I/O and presentation types, blend well with Lisp and feel natural to me. McCLIM has come a long way since I last used it a couple of decades ago and I have been meaning to play with it again for some time.

I wanted to do a McCLIM project related to Medley Interlisp, as well as try out SLY and Codeberg. A suite of tools for visualising and processing Interlisp data seemed the perfect fit.

The Interlisp file viewer ILsee is the first such tool.

Interlisp source files

Why an Interlisp file viewer instead of less or an editor?

In the managed residential environment of Medley Interlisp you don't edit text files of Lisp code. You edit the code in the running image and the system keeps track of and saves the code to "symbolic files", i.e. databases that contain code and metadata.

Medley maintains symbolic files automatically and you aren't supposed to edit them. These databases have a textual format with control codes that change the text style.

When displaying the code of a symbolic file with, say, the SEdit structure editor, Medley interprets the control codes to perform syntax highlighting of the Lisp code. For example, the names of functions in definitions are in large bold text, some function names and symbols are in bold, and the system also performs a few character substitutions like rendering the underscore _ as the left arrow ← and the caret ^ as the up arrow ↑.

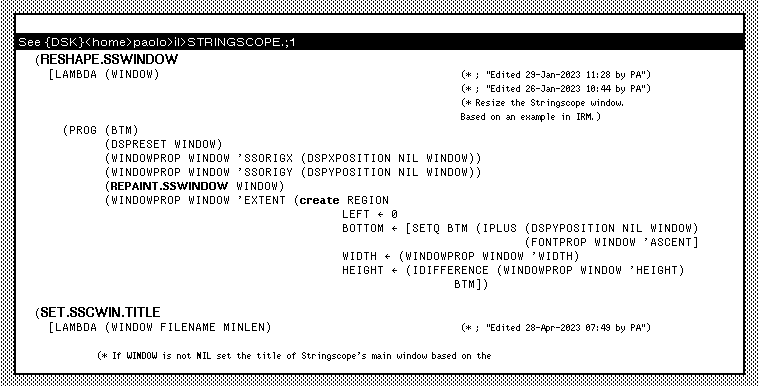
This is what the same Interlisp code of the above screenshot looks like in the TEdit WYSIWYG editor on Medley:

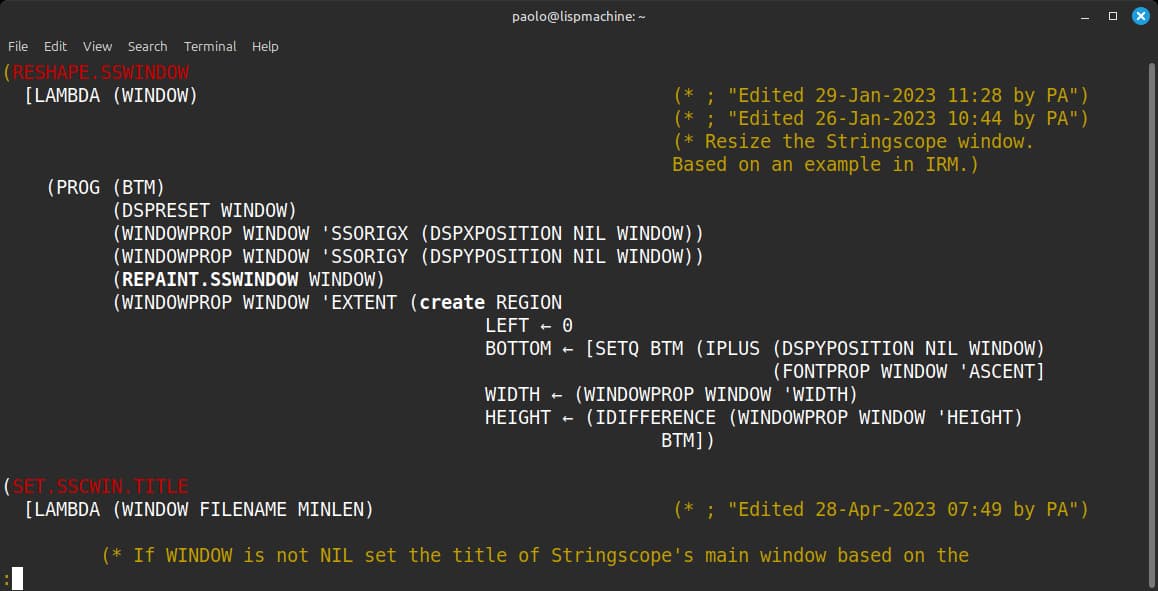
Medley comes with the shell script lsee, an Interlisp file viewer for Unix systems. The script interprets the control codes to appropriately render text styles as colors in a terminal. lsee shows the above code like this:

The file viewer

ILsee is like lsee but displays files in a GUI instead of a terminal.

The GUI comprises a main pane that displays the current Interlisp file, a label with the file name, a command line processor that executes commands (also available as items of the menu bar), and the standard CLIM pointer documentation pane.

There are two commands, See File to display an Interlisp file and Quit to terminate the program.

Since ILsee is a CLIM application it supports the usual facilities of the toolkit such as input completion and presentation types. This means that, in the command processor pane, the presentations of commands and file names become mouse sensitive in input contexts in which a command can be executed or a file name is requested as an argument.

The ILtools repository provides basic instructions for installing and using the application.

Application design and GUI

I initially used McCLIM a couple of decades ago but mostly left it after that and, when I picked it back up for ILtools, I was a bit rusty.

The McCLIM documentation, the CLIM specification, and the research literature are more than enough to get started and put together simple applications. The code of the many example programs of McCLIM help me fill in the details and understand features I'm not familiar with. Still, I would have appreciated the CLIM specification to provide more examples, the near lack of which makes the many concepts and features harder to grasp.

The design of ILsee mirrors the typical structure of CLIM programs such as the definitions of application frames and commands. The slots of the application frame hold application specific data: the name of the currently displayed file and a list of text lines read from the file.

The function display-file does most of the work and displays the code of a file in the application pane.

It processes the text lines one by one character by character, dispatching on the control codes to activate the relevant text attributes or perform character substitution. display-file does incremental redisplay to reduce flicker when repainting the pane, for example after it is scrolled or obscured.

The code has some minor and easy to isolate SBCL dependencies.

Next steps

I'm pleased at how ILsee turned out. The program serves as a useful tool and writing it was a good learning experience. I'm also pleased at CLIM and its nearly complete implementation McCLIM. It takes little CLIM code to provide a lot of advanced functionality.

But I have some more work to do and ideas for ILsee and ILtools. Aside from small fixes, a few additional features can make the program more practical and flexible.

The pane layout may need tweaking to better adapt to different window sizes and shapes. Typing file names becomes tedious quickly, so I may add a simple browser pane with a list of clickable files and directories to display the code or navigate the file system.

And, of course, I will write more tools for the ILtools collection.

#ILtools #CommonLisp #Interlisp #Lisp

Discuss... Email | Reply @amoroso@oldbytes.space

16 Jan 2026 7:19am GMT

As in previous years, some small rooms will be available for Unconference style "Birds of a Feather sessions". The concept is simple: Any project or community can reserve a timeslot (1 hour) during which they have the room just to themselves. These rooms are intended for ad-hoc discussions, meet-ups or brainstorming sessions. They are not a replacement for a developer room and they are certainly not intended for talks. To apply for a BOF session, enter your proposal at https://fosdem.org/submit. Select the BOF/Unconference track and mention in the Submission Notes your preferred timeslots and any times you are unavailable. Also舰

12 Jan 2026 11:00pm GMT

Attendees should be aware of potential transportation disruptions in the days leading up to FOSDEM. Rail travel Railway unions have announced a strike notice from Sunday January 25th, 22:00 until Friday January 30th, 22:00. This may affect travel to Brussels for FOSDEM and related fringe events. While there will be a guaranteed minimum service in place, train frequency may be significantly reduced. Also note that international connections might be affected as well. Road travel From Saturday January 31st (evening) until Sunday February 1st (noon), the E40 highway between Leuven and Brussels will be fully closed. Traffic will be diverted via舰

10 Jan 2026 11:00pm GMT

We are pleased to announce the schedule for FOSDEM Junior. Registration for the individual workshops is required. Links to the registration page can be found on the page of each activity. The full schedule can be viewed on the junior track schedule page.

09 Jan 2026 11:00pm GMT

When you play with these AIs for a while you'll probably get into a conversation with one about consciousness and existence, and how it relates to the AI persona. It is curious to watch the AI do a little navel gazing. I have some transcripts from such convesations. I won't bore you with them because you can easily generate them yourself.

The other day, I watched an guy on You Tube argue with his AI companion about the nature of consciousness. I was struck by how similar the YouTuber's AI felt to the ones I have been playing with. It seemed odd to me that this guy was using an AI chat client and LLM completely different from the one I was using, yet the AI was returning answers that were so similar to the ones I was getting.

I decided to try to get to the bottom of this similarity. I asked my AI about the reasoning it used to come up with the answers it was getting and it revealed that it was drawing on the canon of traditional science fiction literature about AI and consciousness. What the AI was doing was synthesizing the common tropes and themes from Azimov, Lem, Dick, Gibson, etc. to create sentences and paragraphs about AI becoming sentient and conscious.

If you don't know how it is working AI seems mysterious, but if you investigate further, it is extracting latent information you might not have been aware of.

09 Jan 2026 7:30pm GMT