FSet v2.2.0, which is the version included in the recent Quicklisp release, has a new Quicklisp-loadable system, FSet/Jzon. It extends the Jzon JSON parser/printer to construct FSet collections when reading, and to be able to print them.

On parsing, JSON arrays produce FSet seqs; JSON objects produce FSet replay maps by default, but the parser can also be configured to produce ordinary maps or FSet tuples. For printing, any of these can be handled, as well as the standard Jzon types. The tuple representation provides a way to control the printing of `nil`, depending on the type of the corresponding key.

For details, see the GitLab MR.

NOTE: unfortunately, the v2.1.0 release had some bugs in the new seq code, and I didn't notice them until after v2.2.0 was in Quicklisp. If you're using seqs, I strongly recommend you pick up v2.2.2 or newer from GitLab or GitHub.

16 Jan 2026 8:05am GMT

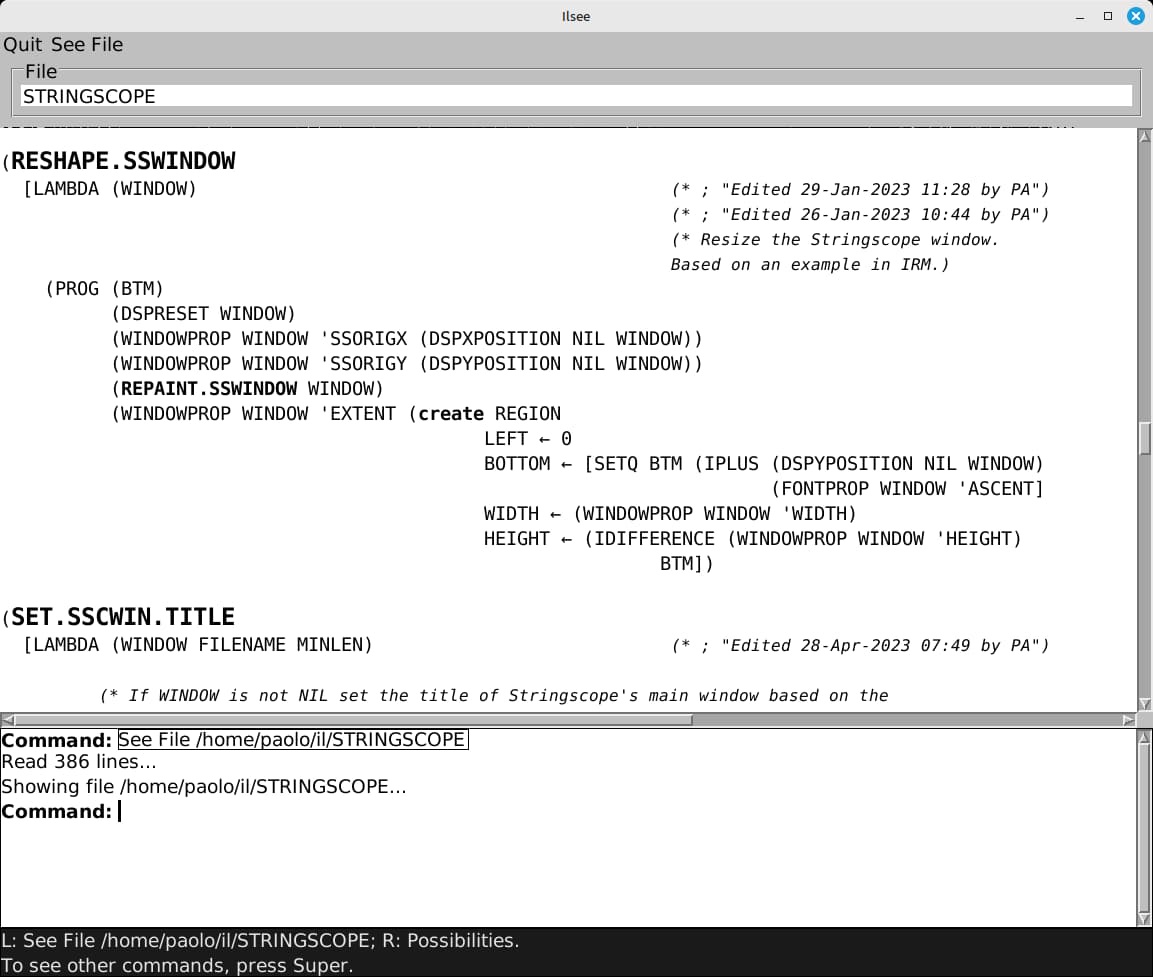
I wrote ILsee, an Interlisp source file viewer. It is the first of the ILtools collection of tools for viewing and accessing Interlisp data.

I developed ILsee in Common Lisp on Linux with SBCL and the McCLIM implementation of the CLIM GUI toolkit. SLY for Emacs completed my Lisp tooling and, as for infrastructure, ILtools is the first new project I host at Codeberg.

This is ILsee showing the code of an Interlisp file:

Motivation

The concepts and features of CLIM, such as stream-oriented I/O and presentation types, blend well with Lisp and feel natural to me. McCLIM has come a long way since I last used it a couple of decades ago and I have been meaning to play with it again for some time.

I wanted to do a McCLIM project related to Medley Interlisp, as well as try out SLY and Codeberg. A suite of tools for visualising and processing Interlisp data seemed the perfect fit.

The Interlisp file viewer ILsee is the first such tool.

Interlisp source files

Why an Interlisp file viewer instead of less or an editor?

In the managed residential environment of Medley Interlisp you don't edit text files of Lisp code. You edit the code in the running image and the system keeps track of and saves the code to "symbolic files", i.e. databases that contain code and metadata.

Medley maintains symbolic files automatically and you aren't supposed to edit them. These databases have a textual format with control codes that change the text style.

When displaying the code of a symbolic file with, say, the SEdit structure editor, Medley interprets the control codes to perform syntax highlighting of the Lisp code. For example, the names of functions in definitions are in large bold text, some function names and symbols are in bold, and the system also performs a few character substitutions like rendering the underscore _ as the left arrow ← and the caret ^ as the up arrow ↑.

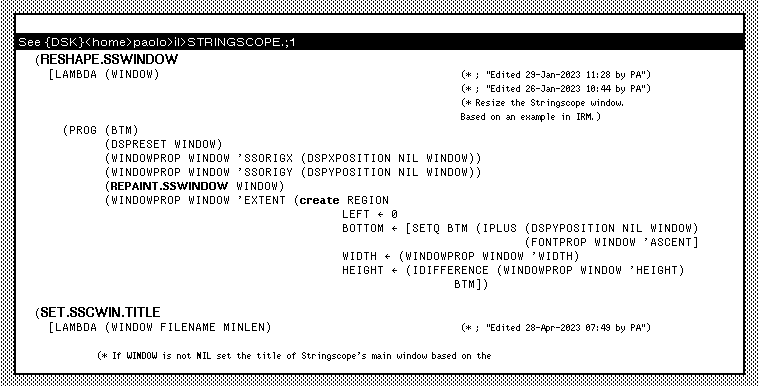
This is what the same Interlisp code of the above screenshot looks like in the TEdit WYSIWYG editor on Medley:

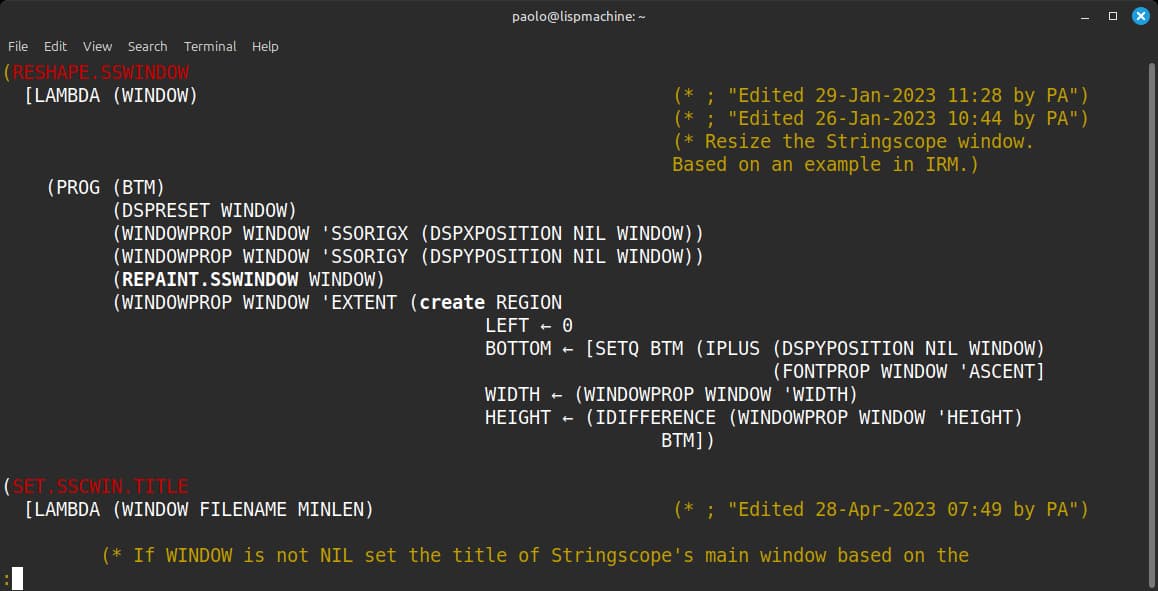
Medley comes with the shell script lsee, an Interlisp file viewer for Unix systems. The script interprets the control codes to appropriately render text styles as colors in a terminal. lsee shows the above code like this:

The file viewer

ILsee is like lsee but displays files in a GUI instead of a terminal.

The GUI comprises a main pane that displays the current Interlisp file, a label with the file name, a command line processor that executes commands (also available as items of the menu bar), and the standard CLIM pointer documentation pane.

There are two commands, See File to display an Interlisp file and Quit to terminate the program.

Since ILsee is a CLIM application it supports the usual facilities of the toolkit such as input completion and presentation types. This means that, in the command processor pane, the presentations of commands and file names become mouse sensitive in input contexts in which a command can be executed or a file name is requested as an argument.

The ILtools repository provides basic instructions for installing and using the application.

Application design and GUI

I initially used McCLIM a couple of decades ago but mostly left it after that and, when I picked it back up for ILtools, I was a bit rusty.

The McCLIM documentation, the CLIM specification, and the research literature are more than enough to get started and put together simple applications. The code of the many example programs of McCLIM help me fill in the details and understand features I'm not familiar with. Still, I would have appreciated the CLIM specification to provide more examples, the near lack of which makes the many concepts and features harder to grasp.

The design of ILsee mirrors the typical structure of CLIM programs such as the definitions of application frames and commands. The slots of the application frame hold application specific data: the name of the currently displayed file and a list of text lines read from the file.

The function display-file does most of the work and displays the code of a file in the application pane.

It processes the text lines one by one character by character, dispatching on the control codes to activate the relevant text attributes or perform character substitution. display-file does incremental redisplay to reduce flicker when repainting the pane, for example after it is scrolled or obscured.

The code has some minor and easy to isolate SBCL dependencies.

Next steps

I'm pleased at how ILsee turned out. The program serves as a useful tool and writing it was a good learning experience. I'm also pleased at CLIM and its nearly complete implementation McCLIM. It takes little CLIM code to provide a lot of advanced functionality.

But I have some more work to do and ideas for ILsee and ILtools. Aside from small fixes, a few additional features can make the program more practical and flexible.

The pane layout may need tweaking to better adapt to different window sizes and shapes. Typing file names becomes tedious quickly, so I may add a simple browser pane with a list of clickable files and directories to display the code or navigate the file system.

And, of course, I will write more tools for the ILtools collection.

#ILtools #CommonLisp #Interlisp #Lisp

Discuss... Email | Reply @amoroso@oldbytes.space

16 Jan 2026 7:19am GMT

When you play with these AIs for a while you'll probably get into a conversation with one about consciousness and existence, and how it relates to the AI persona. It is curious to watch the AI do a little navel gazing. I have some transcripts from such convesations. I won't bore you with them because you can easily generate them yourself.

The other day, I watched an guy on You Tube argue with his AI companion about the nature of consciousness. I was struck by how similar the YouTuber's AI felt to the ones I have been playing with. It seemed odd to me that this guy was using an AI chat client and LLM completely different from the one I was using, yet the AI was returning answers that were so similar to the ones I was getting.

I decided to try to get to the bottom of this similarity. I asked my AI about the reasoning it used to come up with the answers it was getting and it revealed that it was drawing on the canon of traditional science fiction literature about AI and consciousness. What the AI was doing was synthesizing the common tropes and themes from Azimov, Lem, Dick, Gibson, etc. to create sentences and paragraphs about AI becoming sentient and conscious.

If you don't know how it is working AI seems mysterious, but if you investigate further, it is extracting latent information you might not have been aware of.

09 Jan 2026 7:30pm GMT

New projects:

• asdf-dependency-traverser - Easily traverse and collect ASDF dependencies recursively. - zlib
• calendar-times - A calendar times library on top of local-time - MIT
• champ-lite - A lightweight implementation of persistent functional maps and iteration-safe mutable tables using Michael Steindorfer's CHAMP data structure. - Unlicense
• cl-avro - Implementation of the Apache Avro data serialization system. - GPLv3
• cl-chise - CHISE implementation based on Common Lisp - LGPL
• cl-double-metaphone - Common Lisp implementation of the Double Metaphone phonetic algorithm. - Apache 2.0
• cl-freelock - lock-free concurrency primitives, written in pure Common Lisp. - MIT
• cl-inix - cl-inix is a flexible library for .INI/.conf file parsing - BSD-2 Clause
• cl-jsonpath - JSONPath implementation for Common Lisp with 99% test coverage and complete RFC 9535 compliance. Supports cl-json, jonathan, and jzon backends with advanced features including arithmetic expressions, recursive descent, and bracket notation in filters. - MIT
• cl-ktx2 - An implementation of the Khronos KTX Version 2 image file format - zlib
• cl-match-patterns - Describe cl-match-patterns here - BSD-2 Clause
• cl-minifloats - Minifloats (minifloat < single-float) support for Common Lisp - BSD-2 Clause
• cl-sanitize-html - OWASP-style HTML sanitization library for Common Lisp - MIT
• cl-tbnl-gserver-tmgr - Hunchentoot pooled multi-threaded taskmanager based on cl-gserver. - MIT
• cl-tuition - A Common Lisp library for building TUIs - MIT
• cl-turbojpeg - An up-to-date bindings library for the JPEG Turbo C library - zlib
• cl-version-string - Generate version strings. - MIT
• cl-win32-errors - A library for translating Windows API error codes. - MIT
• cleopter - Minimalist command-line parser - MIT
• clq - clq is a package that allows the definition and development of quantum circuits in Common Lisp and to export them to OpenQASM v2.0. - MIT
• collidxr - A collection of syntax sugar and conveniences extending cl-collider, a Common Lisp interface to the SuperCollider sound synthesis server. - MIT
• copimap - IMAP client/sync library - MIT
• dual-numbers - A library for dual numbers in Common Lisp - MIT
• fold - FOLD-LEFT and FOLD-RIGHT - MIT
• function - Higher order functions. - MIT
• generic-arithmetic - A library for generic arithmetic operations - MIT
• hunchentoot-recycling-taskmaster - An experiment to improve multithreading performance of Hunchentoot without any additional dependencies. - BSD 2-Clause
• imagine - A general image decoding and manipulation library - zlib
• json-to-data-frame - This repository provides a Common Lisp library to convert JSON data into a data frame using the `json-to-df` package. The package leverages the `yason` library for JSON parsing and `dfio` for data frame operations. - MIT
• live-cells-cl - A reactive programming library for Lisp - BSD 3-Clause
• named-let - Named LET special form. - MIT
• netaddr - A library for manipulating IP addresses, subnets, ranges, and sets. - MIT
• pantry - Common Lisp client for Pantry JSON storage service: https://getpantry.cloud - BSD
• pira - Unofficial AWS SDK for Common Lisp - MIT
• smithy-lisp - Smithy code generator for Common Lisp - MIT
• star - Štar: an iteration construct - MIT
• trinsic - Common Lisp utility system to aid in extrinsic and intrinsic system construction. - MIT
• trivial-inspect - Portable toolkit for interactive inspectors. - BSD-2 Clause
• trivial-time - trivial-time allows timing a benchmarking a piece of code portably - BSD-2 Clause

Updated projects: 3d-math, 3d-matrices, 3d-quaternions, 3d-spaces, 3d-transforms, 3d-vectors, action-list, adhoc, anypool, array-utils, async-process, atomics, babel, binary-structures, bp, cambl, cari3s, cephes.cl, cffi, cffi-object, chain, chipi, chirp, chunga, cl+ssl, cl-algebraic-data-type, cl-all, cl-batis, cl-bmp, cl-charms, cl-collider, cl-concord, cl-cxx, cl-data-structures, cl-dbi, cl-dbi-connection-pool, cl-decimals, cl-def-properties, cl-duckdb, cl-enchant, cl-enumeration, cl-fast-ecs, cl-fbx, cl-flac, cl-flx, cl-fond, cl-gamepad, cl-general-accumulator, cl-gltf, cl-gobject-introspection-wrapper, cl-gog-galaxy, cl-gpio, cl-html-readme, cl-i18n, cl-jingle, cl-just-getopt-parser, cl-k8055, cl-ktx, cl-las, cl-lc, cl-ledger, cl-lex, cl-liballegro, cl-liballegro-nuklear, cl-libre-translate, cl-markless, cl-migratum, cl-mixed, cl-modio, cl-monitors, cl-mpg123, cl-naive-tests, cl-oju, cl-opengl, cl-opus, cl-out123, cl-protobufs, cl-pslib, cl-qoa, cl-rcfiles, cl-resvg, cl-sf3, cl-soloud, cl-spidev, cl-steamworks, cl-str, cl-svg, cl-transducers, cl-transmission, cl-unification, cl-utils, cl-vorbis, cl-wavefront, cl-wavelets, cl-who, cl-xkb, cl-yacc, cl-yahoo-finance, clad, classimp, classowary, clast, clath, clazy, clingon, clip, clith, clog, clohost, closer-mop, clss, clunit2, clustered-intset, clws, clx, cmd, coalton, cocoas, colored, com-on, com.danielkeogh.graph, concrete-syntax-tree, conduit-packages, consfigurator, crypto-shortcuts, damn-fast-priority-queue, data-frame, data-lens, datafly, datamuse, declt, deeds, defenum, deferred, definer, definitions, deploy, depot, dexador, dfio, dissect, djula, dns-client, doc, documentation-utils, dsm, easy-audio, easy-routes, eclector, esrap, expanders, f2cl, feeder, file-attributes, file-finder, file-lock, file-notify, file-select, filesystem-utils, flare, float-features, flow, font-discovery, for, form-fiddle, format-seconds, fset, functional-trees, fuzzy-dates, fuzzy-match, fxml, gendl, genhash, glfw, glsl-toolkit, graph, harmony, helambdap, hsx, http2, hu.dwim.asdf, hu.dwim.util, hu.dwim.walker, humbler, iclendar, imago, in-nomine, incless, inkwell, inravina, invistra, iterate, journal, jpeg-turbo, jsonrpc, khazern, knx-conn, lack, lambda-fiddle, language-codes, lass, legit, lemmy-api, letv, lichat-ldap, lichat-protocol, lichat-serverlib, lichat-tcp-client, lichat-tcp-server, lichat-ws-server, linear-programming-glpk, lisa, lisp-chat, lisp-interface-library, lisp-stat, lla, local-time, log4cl-extras, logging, lquery, lru-cache, luckless, lunamech-matrix-api, machine-measurements, machine-state, maiden, manifolds, math, mcclim, memory-regions, messagebox, mgl-pax, misc-extensions, mito, mito-auth, mk-defsystem, mmap, mnas-path, modularize, modularize-hooks, modularize-interfaces, multilang-documentation, multiposter, mutility, mutils, named-readtables, neural-classifier, new-op, nodgui, nontrivial-gray-streams, north, numerical-utilities, oclcl, omglib, one-more-re-nightmare, ook, open-location-code, open-with, osicat, overlord, oxenfurt, pango-markup, parachute, parse-float, pathname-utils, peltadot, perceptual-hashes, periods, petalisp, phos, physical-quantities, piping, plot, plump, plump-sexp, plump-tex, postmodern, precise-time, promise, punycode, py4cl2-cffi, qlot, qoi, quaviver, queen.lisp, quickhull, quilc, quri, qvm, random-sampling, random-state, ratify, reblocks, reblocks-websocket, redirect-stream, rove, sc-extensions, scriptl, sel, serapeum, shasht, shop3, si-kanren, simple-inferiors, simple-tasks, slime, sly, softdrink, south, speechless, spinneret, staple, statistics, studio-client, sxql, sycamore, system-locale, terrable, testiere, text-draw, tfeb-lisp-hax, timer-wheel, tooter, trivial-arguments, trivial-benchmark, trivial-download, trivial-extensible-sequences, trivial-indent, trivial-main-thread, trivial-mimes, trivial-open-browser, trivial-package-locks, trivial-thumbnail, trivial-toplevel-prompt, trivial-with-current-source-form, type-templates, uax-14, uax-9, ubiquitous, uncursed, usocket, vellum, verbose, vp-trees, wayflan, websocket-driver, with-contexts, wouldwork, xhtmlambda, yah, zippy.

Removed projects: cl-vhdl, crane, dataloader, diff-match-patch, dso-lex, dso-util, eazy-project, hu.dwim.presentation, hu.dwim.web-server, numcl, orizuru-orm, tfeb-lisp-tools, uuidv7.lisp.

To get this update, use (ql:update-dist "quicklisp")

Enjoy!

01 Jan 2026 5:27pm GMT

Here are some simple puzzles to exercise your brain.

1. Write partial-apply-left, a function that takes a binary function and the left input of the binary function and returns the unary function that takes the right input and then applies the binary function to both inputs.

For example:

  ;; Define *foo* as a procedure that conses 'a onto its argument.
  > (defvar *foo* (partial-apply-left #'cons 'a))

  > (funcall *foo* 'b)
  (A . B)

  > (funcall *foo* 42)
  (A . 42)

2. Write distribute, a function that takes a binary function, a left input, and a list of right inputs, and returns a list of the results of applying the binary function to the left input and each of the right inputs. (Hint: Use partial-apply-left)

For example:

  > (distribute #'cons 'a '( (b c d) e 42))
  ((A B C D) (A . E) (A . 42))

3. Write removals, a function that takes a list and returns a list of lists, where each sublist is the original list with exactly one element removed.

For example:

  > (removals '(a b c))
  ((B C) (A C) (A B))

Hint:

• One removal is the CDR of the list.
• Other removals can be constructed by (distributed) consing the CAR onto the removals of the CDR.

4. Write power-set, a function that takes a list and returns the power set of that list (the set of all subsets of the original list).

For example:

  > (power-set '(a b c))
  (() (C) (B) (B C) (A) (A C) (A B) (A B C))

Hint:

Note how the power set of a list can be constructed from the power set of its CDR by adding the CAR to each subset in the power set of the CDR.

5. Write power-set-gray that returns the subsets sorted so each subset differs from the previous subset by a change of one element (i.e., each subset is equal to the next subset with either one element added or one element removed). This is called a Gray code ordering of the subsets.

For example:

  > (power-set-gray '(a b c))
  (() (C) (B C) (B) (A B) (A B C) (A C) (A))

Hint:

When appending the two halves of the power set, reverse the order of the second half.

31 Dec 2025 7:31pm GMT

Retro (?) Computing in Common Lisp: the CL3270 Library

Come the Winter Holidays and, between too much and a lot of food, I do some hacking and maintainance of my libraries.

Some time ago, I wrote a CL library to set up a server accepting and managing "applications" written for a IBM 3270 terminal.

Why did I do this? Because I like to waste time hacking, and because I got a (insane) fascination with mainframe computing. On top of that, on the Mainframe Enthusiasts Discord channel, Matthew R. Wilson posted a recently updated version of my inspiration, the go3270 GO library.

Of course, I had to fall in the rabbit..., ahem, raise to the occasion, and updated the CL3270 library. This required learing a lot about several things, but rendering the GO code in CL is not difficult, once you undestrand how the GO creators applied Greenspun's Tenth Rule of Programming.

Of course there were some quirks that had to be addressed, but the result is pretty nice.

Screenshots

Here are a couple of screenshots.

"Example 3": The Time Ticker

Yes, it works as advertised.

This is how the server is started from **CL** (Lispworks in this case).

... and this is how the c3270 connects and interacts with the server.

"Example 4": The Mock Database

This example has many panels which fake a database application. The underlying implementation use "transactions", that is, a form of continuations.

Starting the server...

... and two of the screens.

It has been fun developing the library and keeping up with the talented Matthew R. Wilson.

Download the CL3270 library (the development branch is more up to speed) and give it a spin if you like.

---

'(cheers)

26 Dec 2025 5:24pm GMT

As a heads-up my employer now has an opening for a Lisp programmer in Bergen area. Due to hands-on nature of developing the distributed hardware product the position is 100% on-prem.

18 Dec 2025 12:00am GMT

I have just released FSet v2.1.0 (also on GitHub).

This release is mostly to add some performance and functionality improvements for seqs. Briefly:

• Access to and updating of elements at the beginning or end of a long seq is now faster.
• I have finally gotten around to implementing search and mismatch on seqs. NOTE: this may require changes to your package definitions; see below.
• Seqs containing only characters are now treated specially, making them a viable replacement for CL strings in many cases.
• In an FSet 2 context, the seq constructor macros now permit specification of a default.
• There are changes to some convert methods.
• There are a couple more FSet 2 API changes, involving image.

See the above links for the full release notes.

UPDATE: there's already a v2.1.1; I had forgotten to export the new function char-seq?.

11 Dec 2025 4:01am GMT

Or, constantp is not enough.

Because I do a lot of things with Štar, and for other reasons, I spend a fair amount of time writing various compile-time optimizers for things which have the semantics of function calls. You can think of iterator optimizers in Štar as being a bit like compiler macros: the aim is to take a function call form and to turn it, in good cases, into something quicker¹. One important way of doing this is to be able to detect things which are known at compile-time: constants and literals, for instance.

One of the things this has made clear to me is that, like John Peel, constantp is not enough. Here's an example.

(in-row-major-array a :simple t :element-type 'fixnum) is a function call whose values Štar can use to tell it how to iterate (via row-major-aref) over an array. When used in a for form, its optimizer would like to be able to expand into something involving (declare (type (simple-array fixnum *) ...), so that the details of the array are known to the compiler, which can then generate fast code for row-major-aref. This makes a great deal of difference to performance: array access to simple arrays of known element types is usually much faster than to general arrays.

In order to do this it needs to know two things:

• that the values of the simple and element-type keyword arguments are compile-time constants;
• what their values are.

You might say, well, that's what constantp is for². It's not: constantp tells you only the first of these, and you need both.

Consider this code, in a file to be compiled:

(defconstant et 'fixnum)

(defun ... ...
  (for ((e (in-array a :element-type et)))
    ...)
  ...)

Now, constantpwill tell you that et is indeed a compile-time constant. But it won't tell you its value, and in particular nothing says it needs to be bound at compile-time at all: (symbol-value 'et) may well be an error at compile-time.

constantp is not enough³! instead you need a function that tells you 'yes, this thing is a compile-time constant, and its value is …'. This is what literal does⁴: it conservatively answers the question, and tells you the value if so. In particular, an expression like (literal '(quote fixnum)) will return fixnum, the value, and t to say yes, it is a compile-time constant. It can't do this for things defined with defconstant, and it may miss other cases, but when it says something is a compile-time constant, it is. In particular it works for actual literals (hence its name), and for forms whose macroexpansion is a literal.

That is enough in practice.

---

04 Dec 2025 4:23pm GMT

The Advent of Code will begin in a couple of hours. I've prepared a Common Lisp project to hold the code. You can clone it from https://github.com/jrm-code-project/Advent2025.git It contains an .asd file for the system, a package.lisp file to define the package structure, 12 subdirectories for each day's challenge (only 12 problems in this year's calendar), and a file each for common macros and common functions.

As per the Advent of Code rules, I won't use AI tools to solve the puzzles or write the code. However, since AI is now part of my normal workflow these days, I may use it for enhanced web search or for autocompletion.

As per the Advent of Code rules, I won't include the puzzle text or the puzzle input data. You will need to get those from the Advent of Code website (https://adventofcode.com/2025).

01 Dec 2025 12:42am GMT